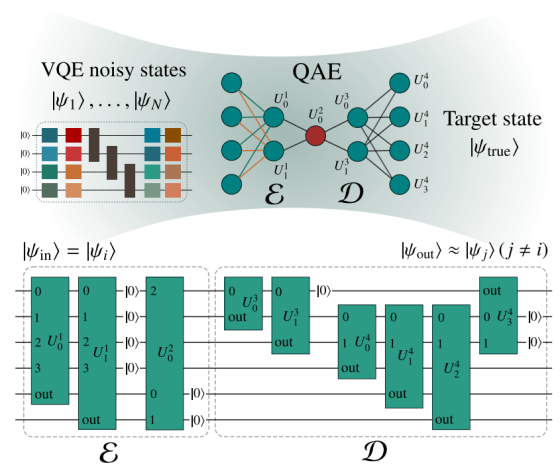
The variational quantum eigensolver (VQE) is a hybrid algorithm that has the potential to provide a quantum advantage in practical … More
Category: Research
Quantum–Classical Hybrid Information Processing via a Single Quantum System
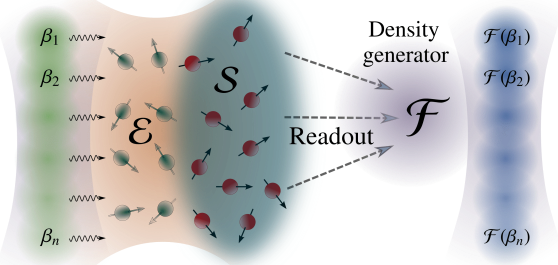
Current technologies in quantum-based communications bring a new integration of quantum data with classical data for hybrid processing. However, the … More
Temporal Quantum Tomography
The impressive progress in realizing quantum-enhanced technologies places a demand on the characterization and validation of quantum hardware. One of … More
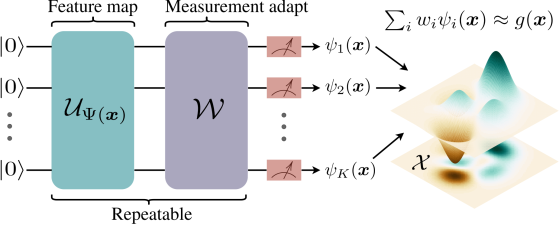
Universal Approximation Property of Quantum Feature Maps
Encoding classical inputs into quantum states is considered a quantum feature map to map classical data into a quantum Hilbert … More
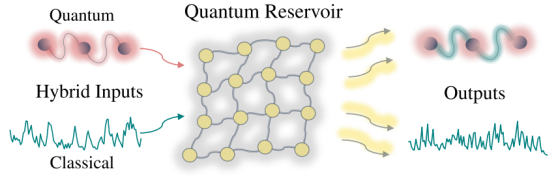
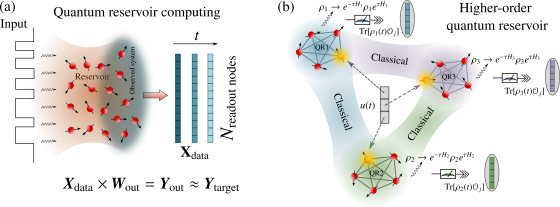
Higher-order Quantum Reservoir Computing
Quantum reservoir computing (QRC) is an emerging paradigm for harnessing the natural dynamics of quantum systems as computational resources that … More
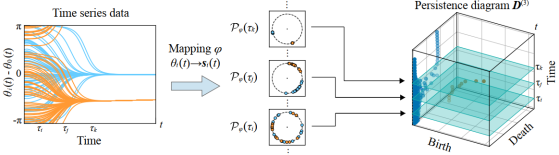
Topological Data Analysis and Coupled Oscillators
The characterization of phase dynamics in coupled oscillators offers insights into fundamental phenomena in complex systems. To describe the collective … More
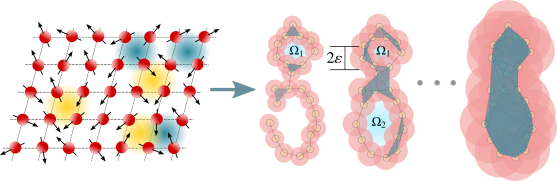
Topological Data Analysis and Phase Transition
The study of phase transitions using is challenging, especially when little prior knowledge of the system is available. Topological data … More
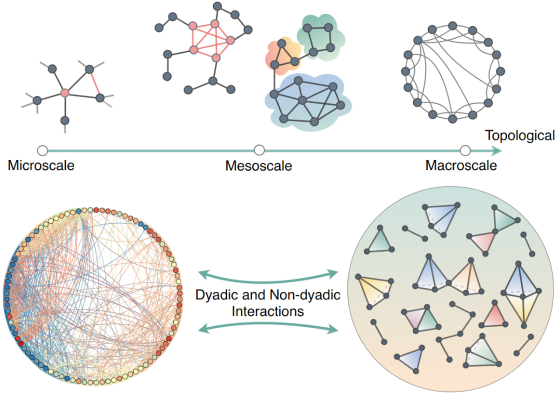
Topology Data Analysis and Complex Networks
Empirical studies have recently shed light on the characteristics of complex networks that are relevant to the dynamics of complex … More
Topology and time-series analysis
Identifying the qualitative changes in time-series data provides insights into the dynamics associated with such data. Such qualitative changes can … More