My name is Tran Quoc Hoan. I am working as a Quantum Researcher at Fujitsu Research. I was a Project…
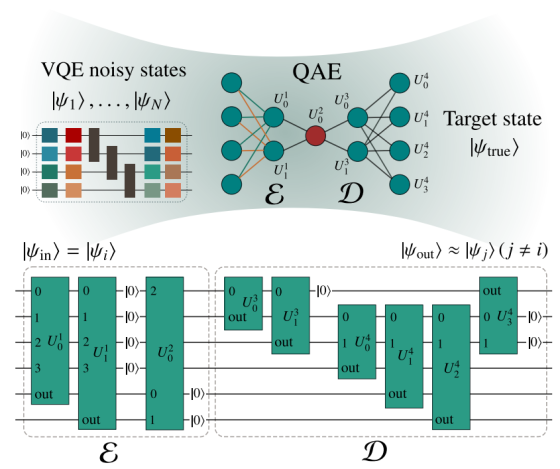
Variational Denoising for Variational Quantum Eigensolver
The variational quantum eigensolver (VQE) is a hybrid algorithm that has the potential to provide a quantum advantage in practical…
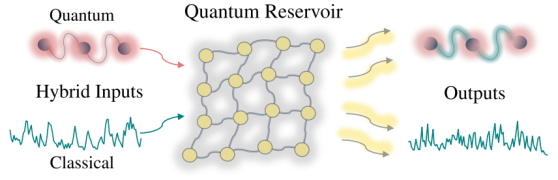
Quantum–Classical Hybrid Information Processing via a Single Quantum System
Current technologies in quantum-based communications bring a new integration of quantum data with classical data for hybrid processing. However, the…
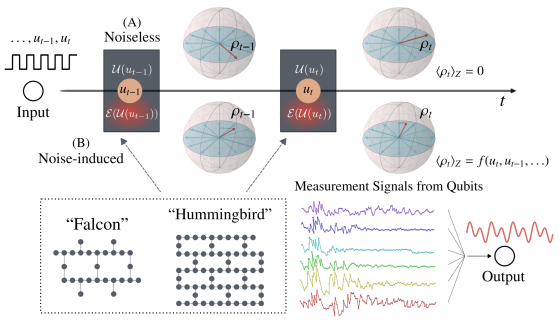
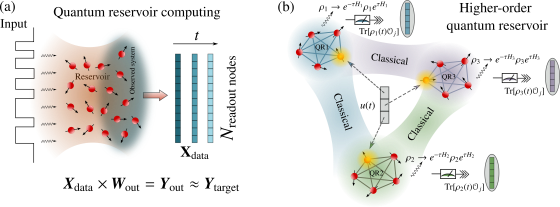
Quantum Noise-Induced Reservoir Computing
Quantum computing has been moving from a theoretical phase to practical one, presenting daunting challenges in implementing physical qubits, which…
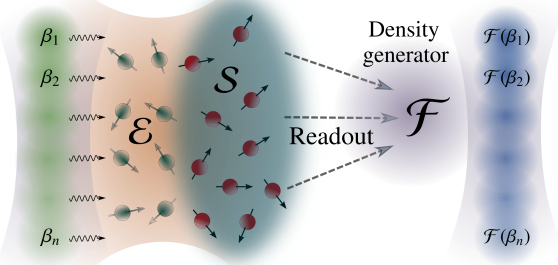
Temporal Quantum Tomography
The impressive progress in realizing quantum-enhanced technologies places a demand on the characterization and validation of quantum hardware. One of…
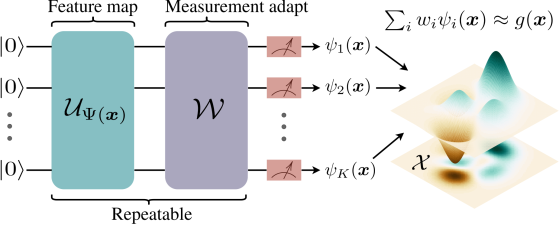
Universal Approximation Property of Quantum Feature Maps
Encoding classical inputs into quantum states is considered a quantum feature map to map classical data into a quantum Hilbert…
Higher-order Quantum Reservoir Computing
Quantum reservoir computing (QRC) is an emerging paradigm for harnessing the natural dynamics of quantum systems as computational resources that…
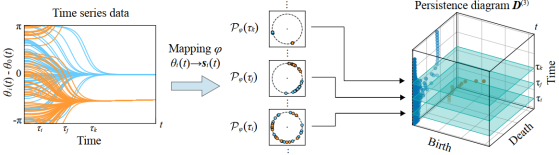
Topological Data Analysis and Coupled Oscillators
The characterization of phase dynamics in coupled oscillators offers insights into fundamental phenomena in complex systems. To describe the collective…
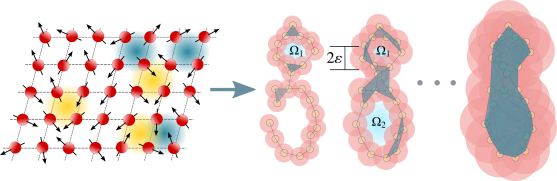
Topological Data Analysis and Phase Transition
The study of phase transitions using is challenging, especially when little prior knowledge of the system is available. Topological data…
Topology Data Analysis and Complex Networks
Empirical studies have recently shed light on the characteristics of complex networks that are relevant to the dynamics of complex…
Topology and time-series analysis
Identifying the qualitative changes in time-series data provides insights into the dynamics associated with such data. Such qualitative changes can…